Jugando con Python y números primos (II)

Buscando patrones

Los número primos parecen impredecibles. ¿Cual es el patrón detrás de los números primos?. Desde hace milenios se está buscando este patrón. Pero hoy contamos con tecnología muy poderosa al alcance de la mano. Contamos con un archivo con gran cantidad de números primos que hicimos en la entrada anterior y con Python que nos permite hacer cálculos y gráficos a gran velocidad.

Busquemos, por ejemplo, la distancia que existe entre números primos. Los primeros números primos son 1, 2 y 3 hay una unidad de distancia entre ellos. Son consecutivos si los miramos en el conjunto de los números enteros. Mientras que 3, 5, 7 tienen dos unidades de distancia entre ellos. Entre 7 y 11 hay 4 unidades y entre 11 y 13 hay sólo 2 unidades de distancia, entre 13 y 17 hay 4 unidades y entre 17 y 19 hay 2. Una sucesión?: 1, 1, 2, 2, 4, 2, 4, 2. Graficando esto tendríamos:

Entendiendo que en el eje x tenemos el consecutivo o sea, el segundo primo (que es 2) tiene una distancia de 1 con el anterior, el tercer primo (que es 3) tiene una distancia de 1 con el anterior, el cuarto primo (que es 5) tiene una distancia de 2 con el anterior y así sucesivamente. El programa en Python que nos permite graficarlo es el siguiente:

import matplotlib.pyplot as plt
import math, time
import numpy as np

primos = [1,2,3,5,7,11,13,17,19]
sucesion = []
anterior = primos[0]
for primo in primos[1:len(primos)]:
    distancia = primo - anterior
    sucesion.append(distancia)
    anterior = primo
for x in sucesion:
    print(x)

# Grafica
fig, ax = plt.subplots()
plt.scatter(range(2, len(sucesion)+2), sucesion)
ax.set_xlabel('Consecutivo primo')
ax.set_ylabel('Distancia')
plt.show()

No tenemos en cuenta el primer primo y comenzamos a calcular distancias desde el segundo, por ello en el bucle for comenzamos en el elmento 1 no en el cero (0) que se lo hemos asignado a la variable anterior:

anterior = primos[0]
for primo in primos[1:len(primos)]:

Y por ello tambien al momento de graficar comenzamos por 2 y le sumamos 2 al final del eje en la línea:

plt.scatter(range(2, len(sucesion)+2), sucesion)

La función plt.scatter grafica los puntos. Recibe dos argumentos: la lista con los puntos para el eje x, y la lista con los puntos para el eje y. La lista para x la hacemos con la funcion range, dándole dos argumenos, inicio y final del rango: comienza en 2 y termina en la longitud mas 2 de la lista sucesion que contiene las distancias que queremos examinar. Para el eje y basta con darle la lista sucesion que creamos en el bucle for inicial.

Si trazamos una línea entre los puntos de pronto podremos ver mejor algún patrón escondido Ello lo hacemos con la función plt.plot. Agregamos la siguiente instrucción justo debajo de plt.scatter:

plt.plot(range(2, len(sucesion)+2), sucesion)

Y obtenemos la siguiente gráfica:

Recordemos que el eje x no representa un número primo sino un consecutivo (el primer primo, el segundo primo, el tercer primo,…, el i-esimo primo, etc.) y el eje y, la distancia entre el i-esimo número primo y el anterior.

¿No ve aún el patrón?, bueno 8 puntos son muy pocos. Pero no seamos tímidos, tenemos un archivo con 50 millones de puntos. Intentemos hacer el gráfico con ellos. A lo mejor detectamos algo.

Leyendo los puntos del archivo

En la entrada anterior generamos un archivo con gran cantidad de números primos. Si descomprimimos el archivo (se requiere espacio en disco por que tiene mas de 500 megas) tendremos un archivo con extensión htm. Es conveniente cambiar la extensión a .txt por razones de estandarización. Si usted mismo lo generó usando el programa de la entrada anterior, pues ya tendrá en su disco el archivo con el nombre que le haya asignado. Visualizar un archivo tan grande suele ser dificil con el block de notas, sugiero usar el software EditPad Lite que es muy liviano y gratuito para uso personal.

Para leer el archivo desde Python construiremos una función que nos permita leerlo y almacenar su contenido (total o parcialmente) en una lista.

def lee_primos(cantidad, inicio = 0):
    f_in = 'primos_hasta_1000000000.txt'
    f = open(f_in, 'r')
    contador = 0 # Numeros almacenados en la lista
    indice = 0 # Registros leídos del archivo
    primos = []
    
    for numero in f:
        if indice >= inicio:
            primos.append(int(numero))
            if contador == cantidad:
                break
            contador += 1
        indice += 1
    return primos

Esta función tendrá la flexibilidad para entregarnos un subconjunto de números primos. El primer parámetro permite indicarle cuantos números del archivo queremos extraer. El parámetro inicio, que es opcional y por omisión tiene el valor 1, permite indicarle desde cual queremos iniciar: el primero o el milésimo. Si llamamos la función:

lee_primos(500, inicio = 1000)

Estamos recuperando 500 números primos del archivo a partir del que se encuentra en la posición 1000. Mientras que si sólo escribimos:

lee_primos(500)

Estamos extractando los primeros 500 números primos.

Hagamos también una función para graficar de forma que podamos llamarla tantas veces como queramos:

# Grafica
def grafica(sucesion,  desde=1):
    fig = plt.figure()
    ax = fig.add_subplot(211)
    ex = plt.subplot(1,1,1)
    plt.scatter(range(desde, len(sucesion)+desde), sucesion)
    plt.plot(range(desde, len(sucesion)+desde), sucesion, linewidth ='0.2')
    ex.set_xlabel('Consecutivo primo')
    ex.set_ylabel('Distancia')
    ex.set_title('Distancia entre primos desde el '+str(desde)+' hasta '+str(desde+len(sucesion)-1))

Esta función recibe un parametro obligatorio y uno opcional. El obligatorio es la lista de distancias a graficar, se recibe en la variable sucesion. La segunda variable (opcional) indica en qué número debe comenzar el eje x, o sea desde cual consecutivo se envía la sucesión.

El cálculo de la distancia entre números primos es el ciclo for que vimos al iniciar esta entrada. Haremos una función con este bucle para poderlo reusar:

# Genera lista de distancias
def sucesion_distancias(lista_primos):
    sucesion = []
    anterior = lista_primos[0]
    for primo in lista_primos[1:len(primos)]:
        distancia = primo - anterior
        sucesion.append(distancia)
        anterior = primo
    return sucesion

Listo. Sólo nos queda el programa principal, Definiremos unos parámetros como el número de puntos a graficar y desde cual consecutivo comenzaremos:

# Parametros
consecutivo_inicial = 1000   # Desde cuál consecutivo comienza
cantidad = 100    # Cuantos primos graficará

Para este ejemplo estamos graficando 100 puntos comenzando por el primo ubicado en la posición mil. A continuación llamamos a la función lee_primos y almacenamos la lista generada en la variable sucesion.Esta variable la usamos como entrada en la función grafica, por último mostramos la gráfica con plt.show().

primos = lee_primos(cantidad, inicio=consecutivo_inicial)
sucesion = sucesion_distancias(primos)
grafica(sucesion, desde = consecutivo_inicial)

plt.show()

El programa completo sería el siguiente:

import matplotlib.pyplot as plt
import math, time
import numpy as np

#------------ Funciones -----------------------------------
# Grafica
def grafica(sucesion,  desde=1):
    fig = plt.figure()
    ax = fig.add_subplot(211)
    ex = plt.subplot(1,1,1)
    plt.scatter(range(desde, len(sucesion)+desde), sucesion)
    plt.plot(range(desde, len(sucesion)+desde), sucesion, linewidth ='0.2')
    ex.set_xlabel('Consecutivo primo')
    ex.set_ylabel('Distancia')
    ex.set_title('Distancia entre primos desde el '+str(desde)+' hasta '+str(desde+len(sucesion)-1))
    

# Lee del archivo
def lee_primos(cantidad, inicio = 1):
    f_in = 'primos_hasta_1000000000.txt'
    f = open(f_in, 'r')
    contador = 0 # Numeros almacenados en la lista
    indice = 0 # Registros leídos del archivo
    primos = []
    
    for numero in f:
        if indice >= inicio:
            primos.append(int(numero))
            if contador == cantidad:
                break
            contador += 1
        indice += 1
    return primos

# Genera lista de distancias
def sucesion_distancias(lista_primos):
    sucesion = []
    anterior = lista_primos[0]
    for primo in lista_primos[1:len(primos)]:
        distancia = primo - anterior
        sucesion.append(distancia)
        anterior = primo
    return sucesion
#---------------------------------------------------------------
# Parametros
consecutivo_inicial = 1000   # Desde cuál consecutivo comienza
cantidad = 100    # Cuantos primos graficará
primos = lee_primos(cantidad, inicio=consecutivo_inicial)
sucesion = sucesion_distancias(primos)
grafica(sucesion, desde = consecutivo_inicial)

plt.show()

Y obtenemos nuestra gráfica de 100 puntos comenzando en el milesimo primo:

Dijimos que no seríamos tímidos, podemos intentarlo con un millón de puntos:

# Parametros
consecutivo_inicial = 1000   # Desde cuál consecutivo comienza
cantidad = 1000000    # Cuantos primos graficará

Se ven algunas cosas interesantes. Muchas distancias están entre 2 y 60, un poco menos entre 60 y 100 y pocas son mayores que 100. ¿Será así para el intervalo entre digasmos 10 millones y 11 millones?. Miremos:

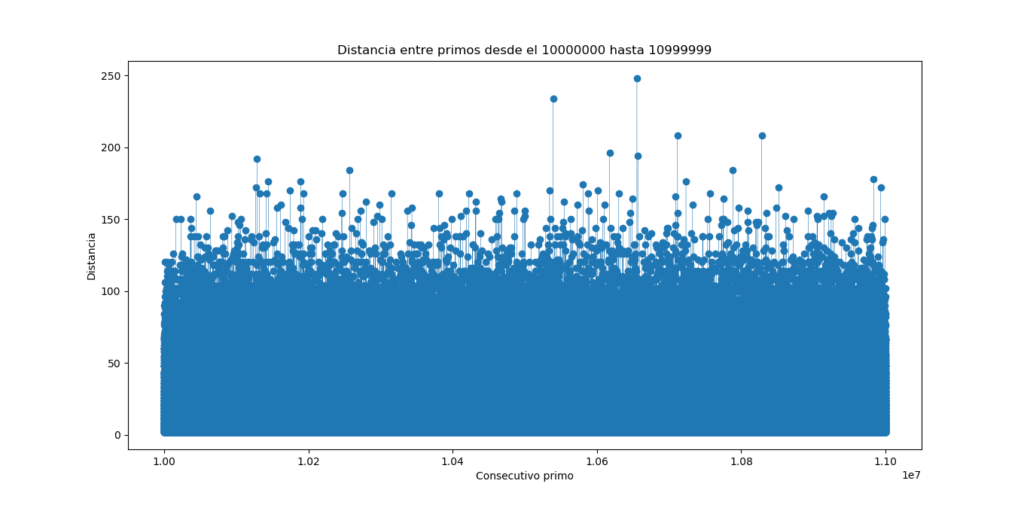
Aquí se ven muchos puntos con distancias entre 2 y 100, no tantos entre 100 y 150 y pocos mayores que 150. Significa esto que cada vez hay mas distancia entre los números primos?, en consecuencia hay menos números en intervalos superiores?

Tendremos que hacer conteos para averiguarlo, pero esta entrada ya está muy larga, lo dejamos para la próxima semana.

Generando Números Primos Promedios de las distancias